February 4, 2025
4 min learn
Mathematicians Resolve Notorious ‘Transferring Couch Drawback’
What’s the most important sofa that may flip a nook? After 58 years, we lastly know

For many who have wrestled a cumbersome sofa round a good nook and lamented, “Will this even match?” mathematicians have heard your pleas. Geometry’s “shifting couch drawback” asks for the most important form that may flip a proper angle in a slim hall with out getting caught. The issue sat unsolved for practically 60 years till November, when Jineon Baek, a postdoc at Yonsei College in Seoul, posted a paper on-line claiming to resolve it. Baek’s proof has but to bear thorough peer assessment, however preliminary passes from mathematicians who know Baek and the shifting couch drawback appear optimistic. Solely time will inform why it took Baek 119 pages to write down what Ross Geller of the sitcom Pals stated in a single phrase.
The answer is unlikely that can assist you on shifting day, however as frontier math grows extra abstruse, mathematicians maintain a particular fondness for unsolved issues that anyone can perceive. In truth, the favored math discussion board MathOverflow maintains an inventory of “Not particularly well-known, long-open issues which anybody can perceive,” and the shifting couch drawback at the moment ranks second on the checklist. Nonetheless, each proof expands our understanding, and the strategies used to resolve the shifting couch drawback will probably lend themselves to different geometric puzzles down the highway.
The principles of the issue, which Canadian mathematician Leo Moser first formally posed in 1966, contain a inflexible form—so the cushions don’t yield when pressed—turning a proper angle in a hallway. The couch could be any geometric form; it doesn’t should resemble an actual sofa. Each the form and the hallway are two-dimensional. Think about the couch weighs an excessive amount of to carry, and you may solely slide it.
On supporting science journalism
When you’re having fun with this text, take into account supporting our award-winning journalism by subscribing. By buying a subscription you’re serving to to make sure the way forward for impactful tales in regards to the discoveries and concepts shaping our world at this time.
A fast tour by means of the issue’s historical past reveals the intensive effort that mathematicians have poured into it—they have been no sofa potatoes. Confronted with an empty hallway, what’s the largest form you may squeeze by means of it? If every leg of the hall measures one unit throughout (the precise unit doesn’t matter), then we are able to simply scoot a one-by-one sq. by means of the passage. Elongating the sq. to type a rectangle fails immediately, as a result of as soon as it hits the kink within the hallway, it has no room to show.
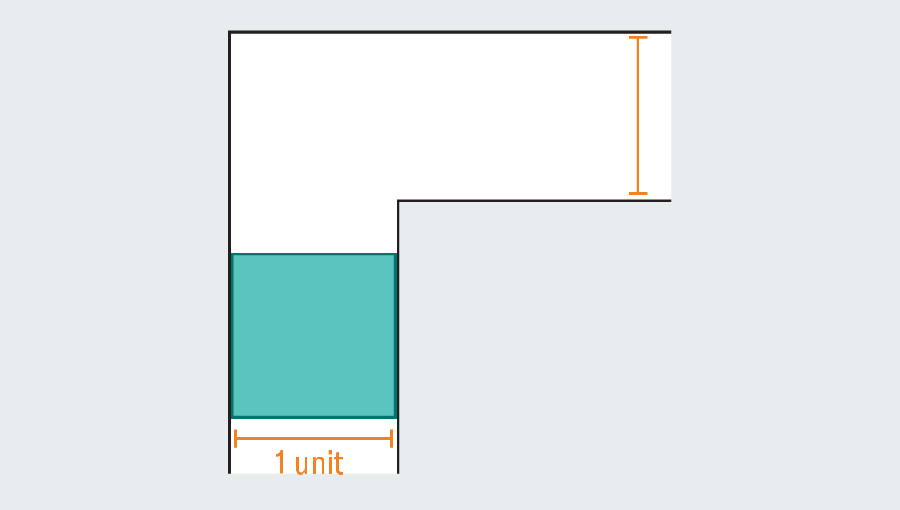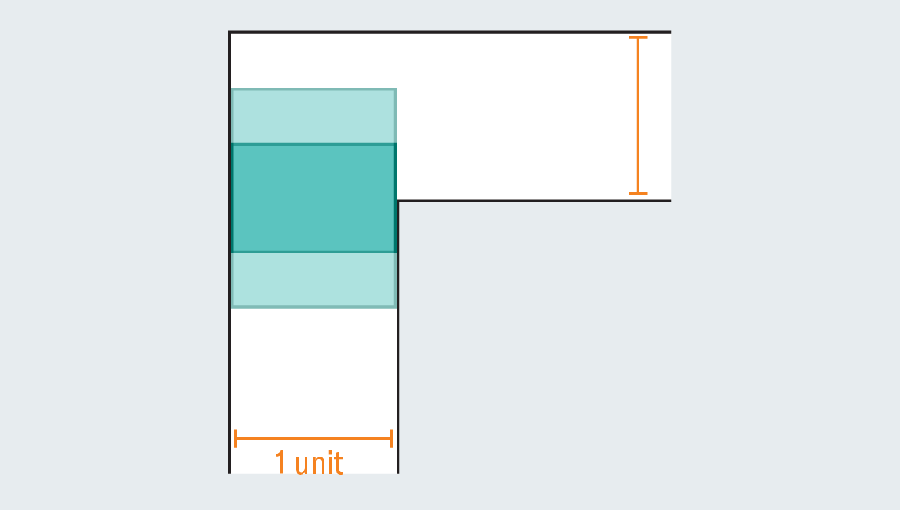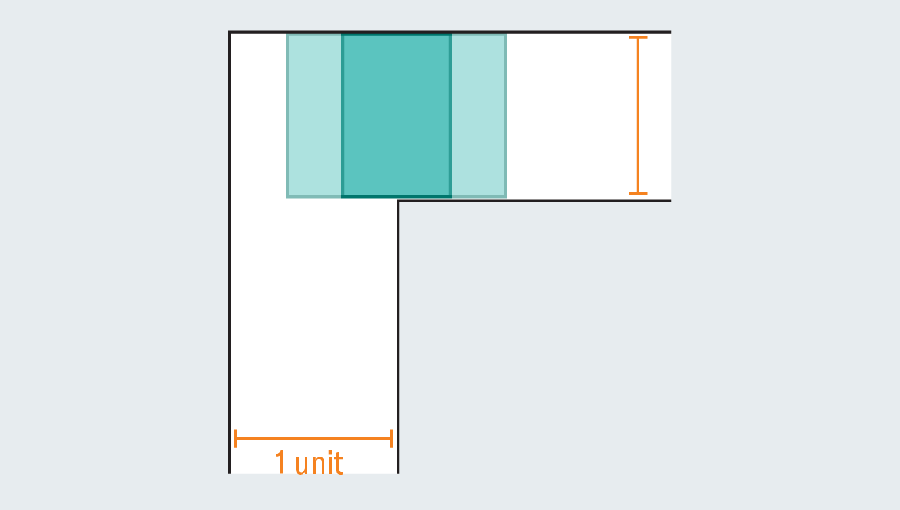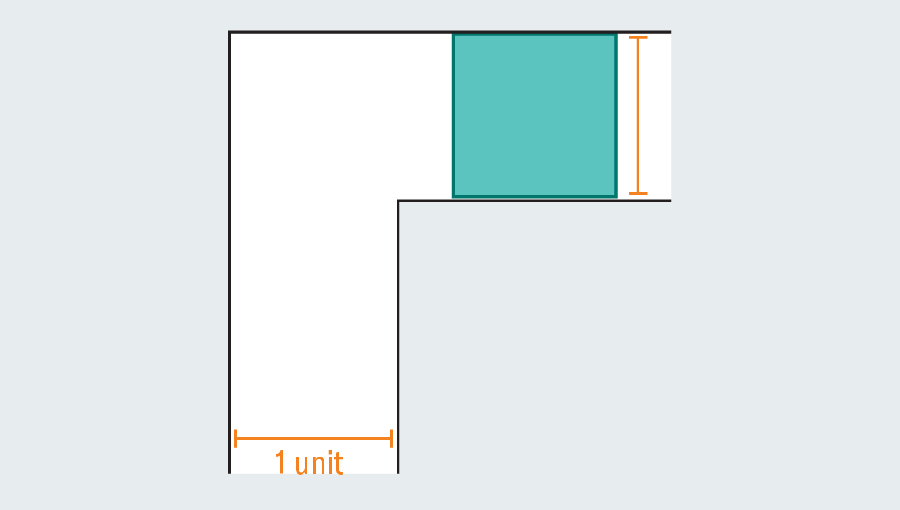
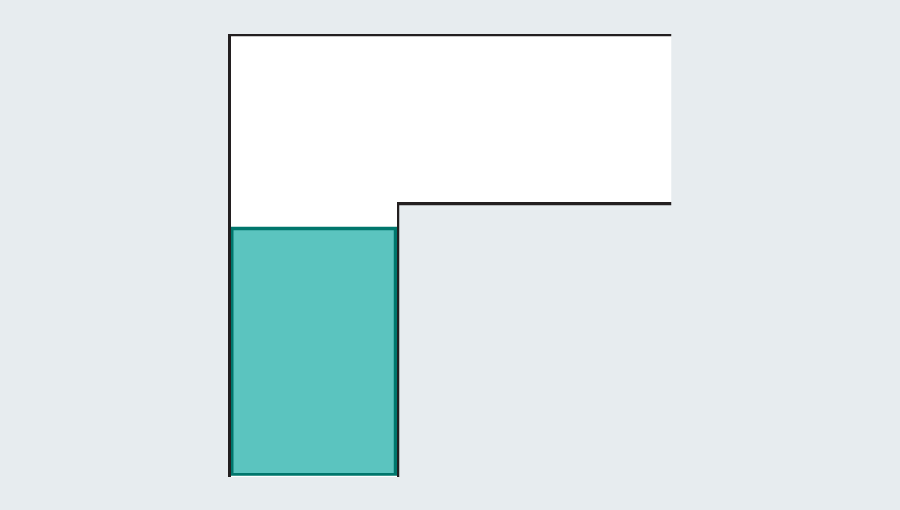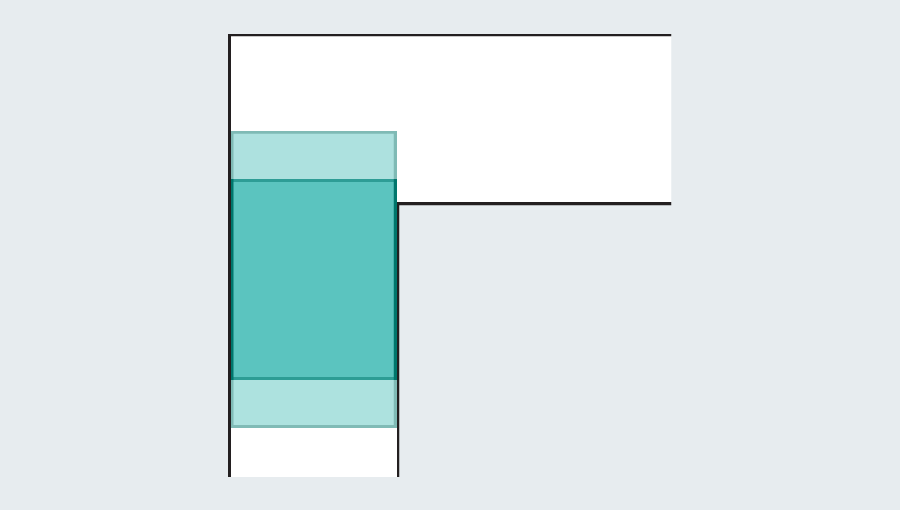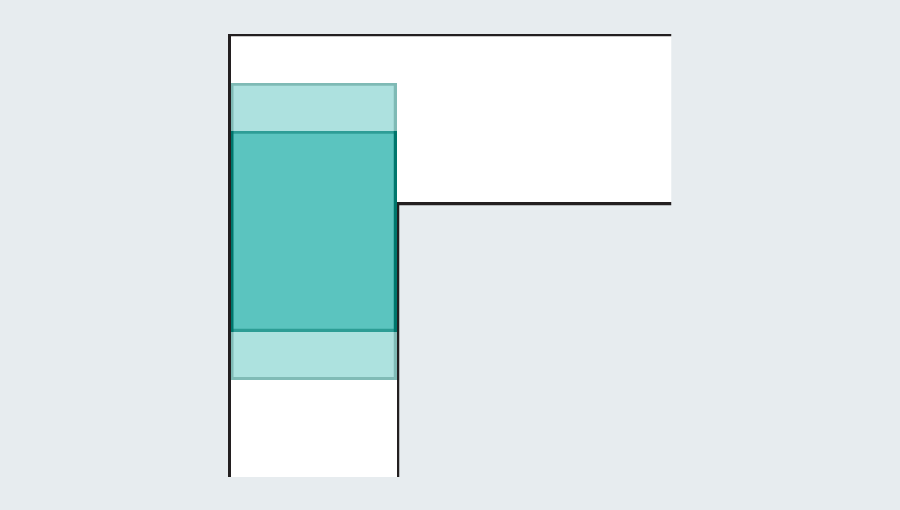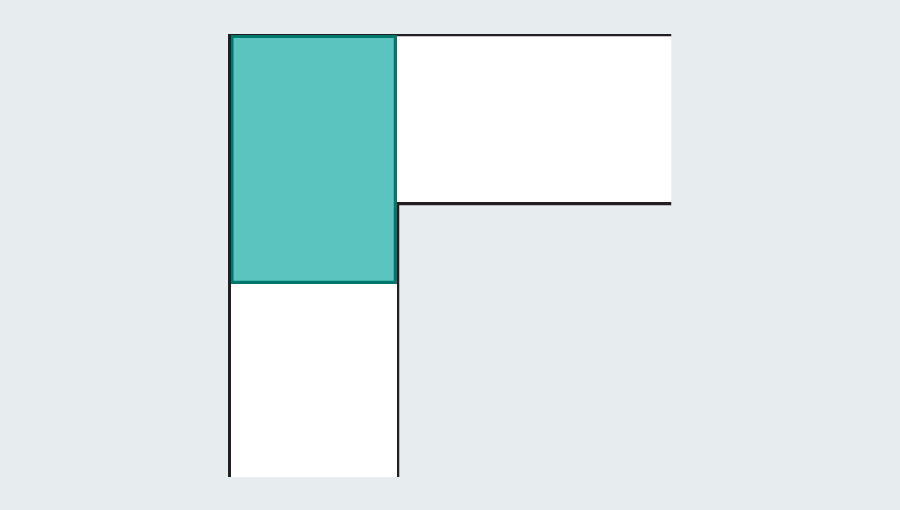
But mathematicians realized they’ll go larger by introducing curved shapes. Contemplate a semicircle with a diameter (the straight base) of two. When it hits the flip, a lot of it nonetheless overhangs within the first leg of the hallway, however the rounded edge leaves simply sufficient room to clear the nook.
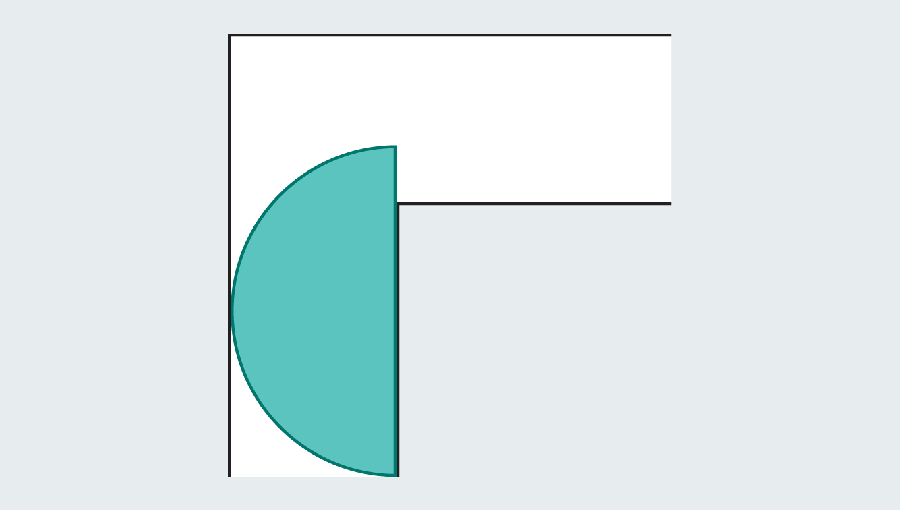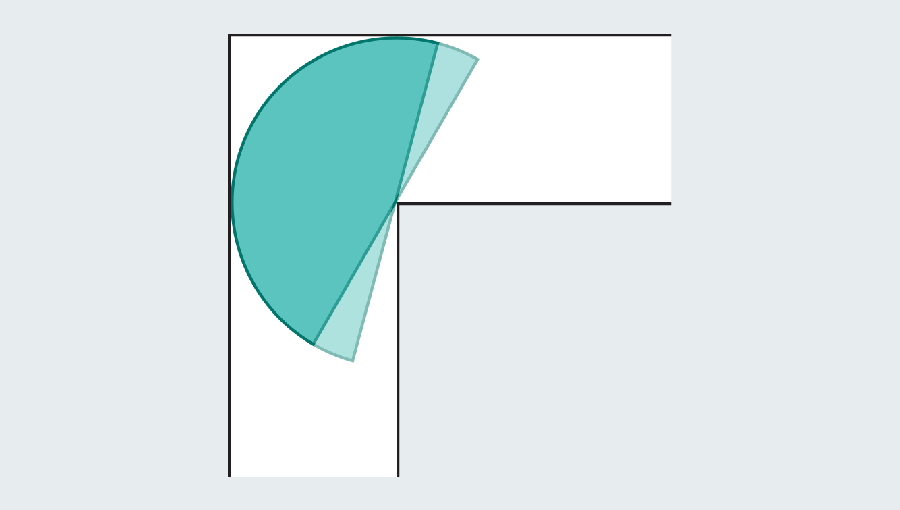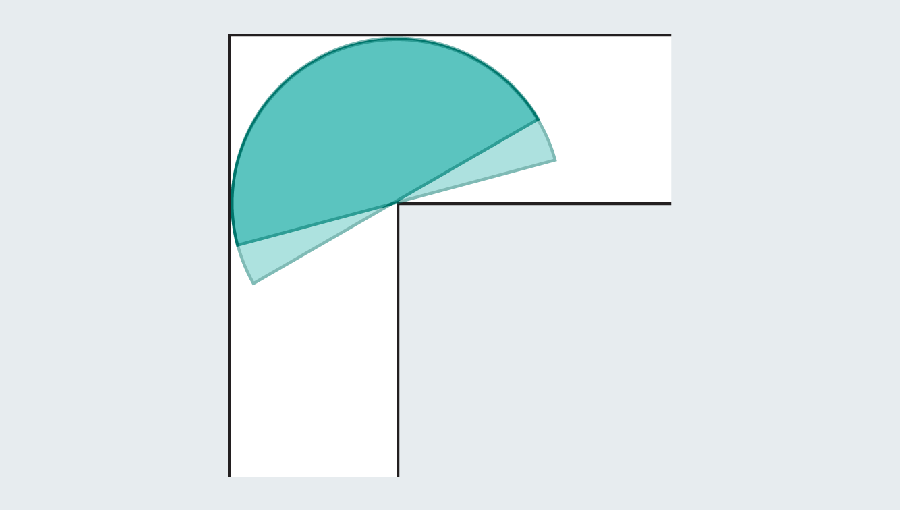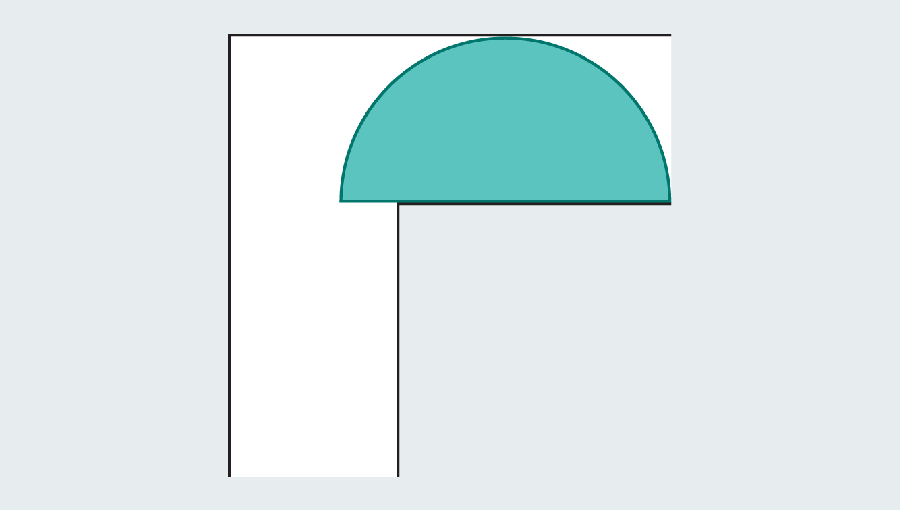
Bear in mind the objective is to seek out the most important “sofa” that slides across the nook. Dusting off our highschool geometry formulation, we are able to calculate the realm of the semicircle as π/2, or roughly 1.571. The semicircle provides a major enchancment over the sq., which had an space of only one. Sadly each would look unusual in a lounge.
Fixing the shifting couch drawback requires that you simply not solely optimize the dimensions of a form, but in addition the trail that form traverses. The setup permits two varieties of movement: sliding and rotating. The sq. sofa solely slid, whereas the semicircle slid, then rotated across the bend, after which slid once more on the opposite facet. However objects can slide and rotate on the similar time. Mathematician Dan Romik of the College of California, Davis, has famous {that a} answer to the issue ought to optimize each varieties of movement concurrently.
British mathematician John Hammersley found in 1968 that stretching the semicircle can purchase you a bigger couch in case you carve out a bit to take care of that pesky nook. Moreover, Hammersley’s couch takes benefit of a hybrid sliding plus rotating movement. The ensuing couch seems like a landline phone:

Amanda Montañez; Supply: “On Transferring a Couch Round a Nook,” by Joseph L. Gerver, in Geometriae Dedicata, Vol. 42, No. 3; June 1992 (reference)
Optimizing the totally different variables yields a settee with space π/2 + 2/π, or roughly 2.2074. It is a enormous improve from the semicircle, akin to shifting from a love seat to a sectional. However progress stalled there for twenty-four years. The subsequent vital enchancment could be the final. In 1992 Joseph Gerver unveiled a masterwork of mathematical carpentry, which we now know to be the most important attainable couch.
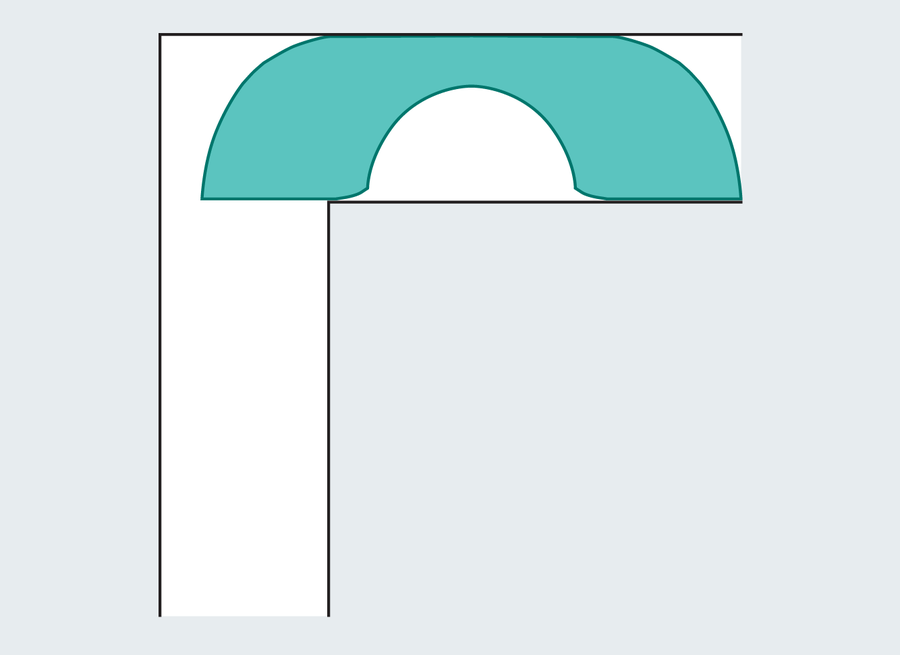
Amanda Montañez; Supply: “On Transferring a Couch Round a Nook,” by Joseph L. Gerver, in Geometriae Dedicata, Vol. 42, No. 3; June 1992 (reference)
You’d be forgiven for feeling déjà vu proper now. Gerver’s couch seems an identical to Hammersley’s, but it surely’s a way more difficult building. Gerver stitched collectively 18 distinct curves to type his form. On nearer inspection you would possibly spot some variations, particularly the beveled edges on the base of the rounded cutout.
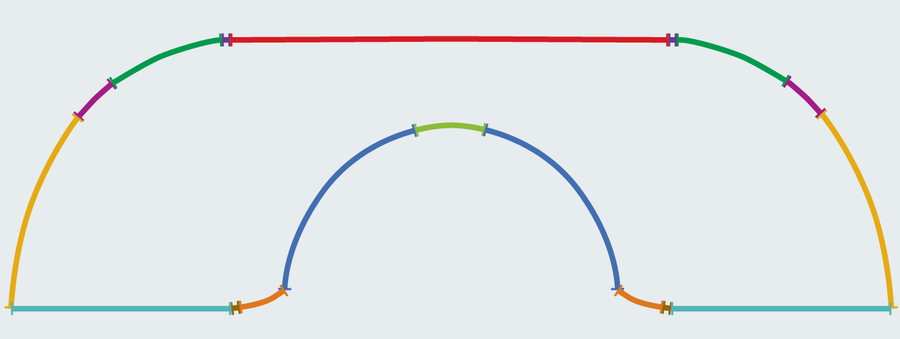
Amanda Montañez; Supply: “On Transferring a Couch Round a Nook,” by Joseph L. Gerver, in Geometriae Dedicata, Vol. 42, No. 3; June 1992 (reference)
The realm of Gerver’s triumph measures in at 2.2195 models. Surprisingly, Hammersley’s comparatively easy couch solely fell about .012 in need of optimum. Though solely a skosh bigger than its predecessor, Gerver suspected that his discovery reached the utmost attainable measurement. He couldn’t show it although. And neither might anyone else for one more 32 years.
Baek completed his Ph.D. in 2024 and wrote his thesis on the shifting couch drawback, contributing a number of incremental insights. That very same 12 months, he sewed all of his contemporary concepts collectively into a powerful opus that proves no couch bigger than Gerver’s can squeeze by means of the hallway. Cracking a long-standing open drawback is a dream for any mathematician, not to mention one so early of their profession. If Baek’s work withstands scrutiny, he’ll probably discover himself in excessive demand for professorships. Except he pivots into furnishings making.
